1D spectra utilities
1D spectra utilities#
ENSDF reader#
The ENSDF reader allows to read, from the TkN library, all ENSDF/XUNDL databases and to plot on top of the displayed histogram arrows corresponding to the known transitions.
Write the name of the nucleus you want to plot and press enter to validate. This will gives something as:
By default, the ENSDF dataset "ADOPTED LEVELS, GAMMAS" is used. This contains all the known gamma rays, combining all the nucleus production methods (\(\beta\)-decay, coulex, fission...). This is possible to select the desired dataset using the ENSDF data-set list. In the following figure, the dataset has been changed to Uranium fission, limitating drastically the number of \(\gamma\)-rays.
In this last plot, the option "Full title" has been used to print more information on the \(\gamma\)-rays. Some parameters can be used to filter the type of decays to be shown.
Peak fitter#
The Peak fitter utility is composed of four sub parts:
Peak search#
The peak search is a one-dimensional peak search tool based on the ROOT TSpectrum class. Sigma is the sigma of searched peaks while threshold remove all peaks with amplitude less than threshold x highest_peak
If you change the parameters, remember to clear the present peaks (Clear button) before starting a new search.
Minimizer#
The two last utilities are based on ROOT fits. The minimizer allows to define which minimize will to be used for the fits. The Fit options can contain any options from ROOT standard fit options. The default value "I" is to use the integral of the function in the bin instead of the default bin center value. For more details on the options, see the ROOT documentation.
Background Fit#
The background fit is a tool to be used when the statistics is too low to perform a good fit. The idea is to determine a range before and after the peak (four arrows) that will be used to fit the backgroud. The peak area is then determined using the histogram area minus the area of the fitted background.
If the efficiency function has been defined in the current Workspace, the area will also be printed corrected from the detector's efficiency. The position of the maximum in the fit range will be used for the energy determination.
To define the background ranges, click on Set and define the four limits of the background (2 arrows for the range before the peak and two after).
Two types of background can be used, a 1rst order polynomial and/or and exponential function.
Then click on Fit:
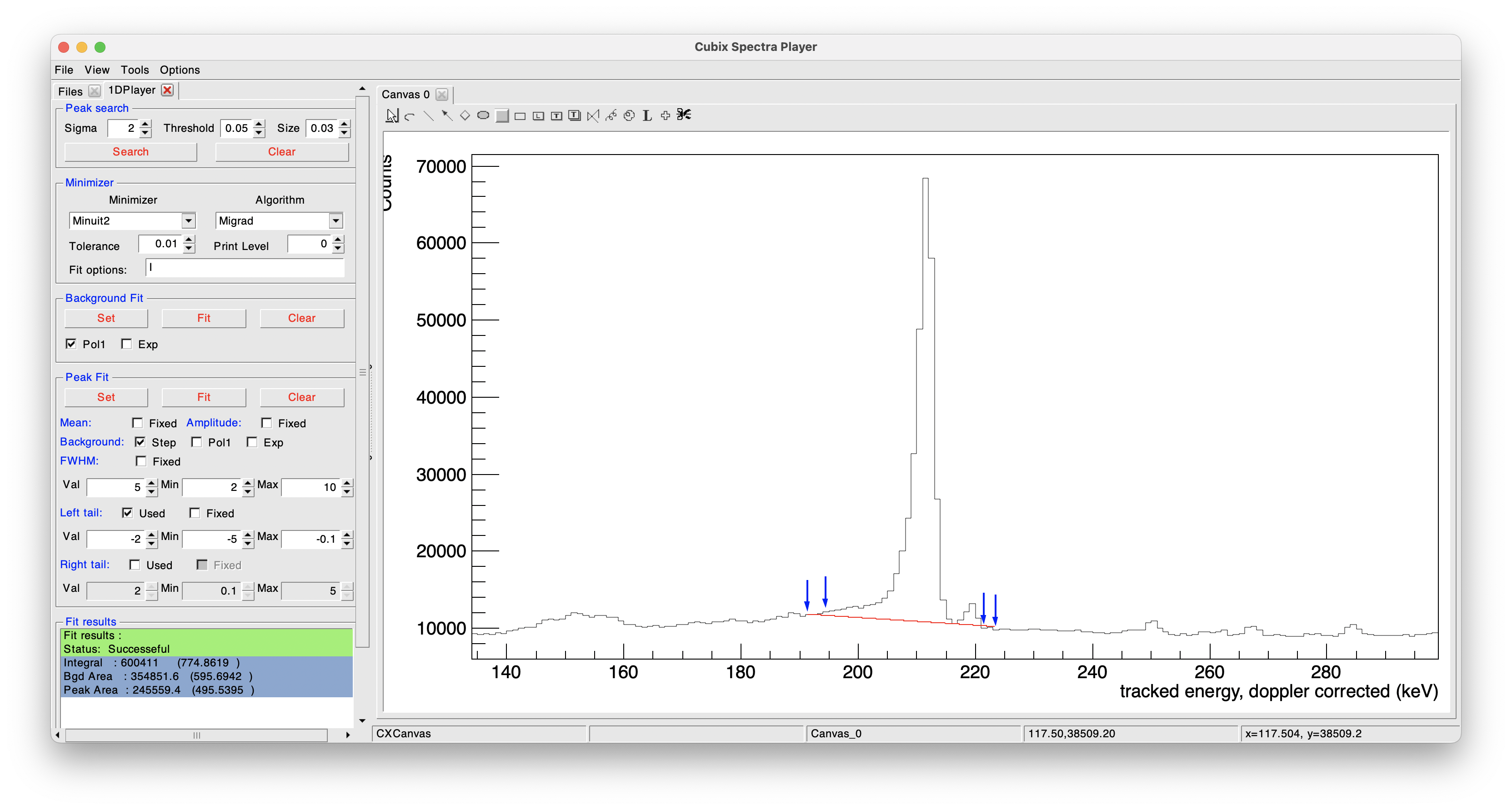
The obtained integral is printed in the terminal and in the cubix window.
PeakFit#
The peak fit allows to fit a gaussian peak. As this software is dedicated to \(\gamma\)-ray spectroscopy, the default function suppose a gaussian peak, with a possible left and right tail (for taking into account possible neutron damage in the detectors or lifetime effects), and a step background to take into account the Compton part bellow the peak.
To define a peak (or multpiple peaks), you need to click on Set and then click on the positions of the background range (before and after the peak(s)).
The order is not important, the lowest/highest values will be taken as background, and all the others arrows will be considered as peaks.
Click then on Fit to perform the fit:
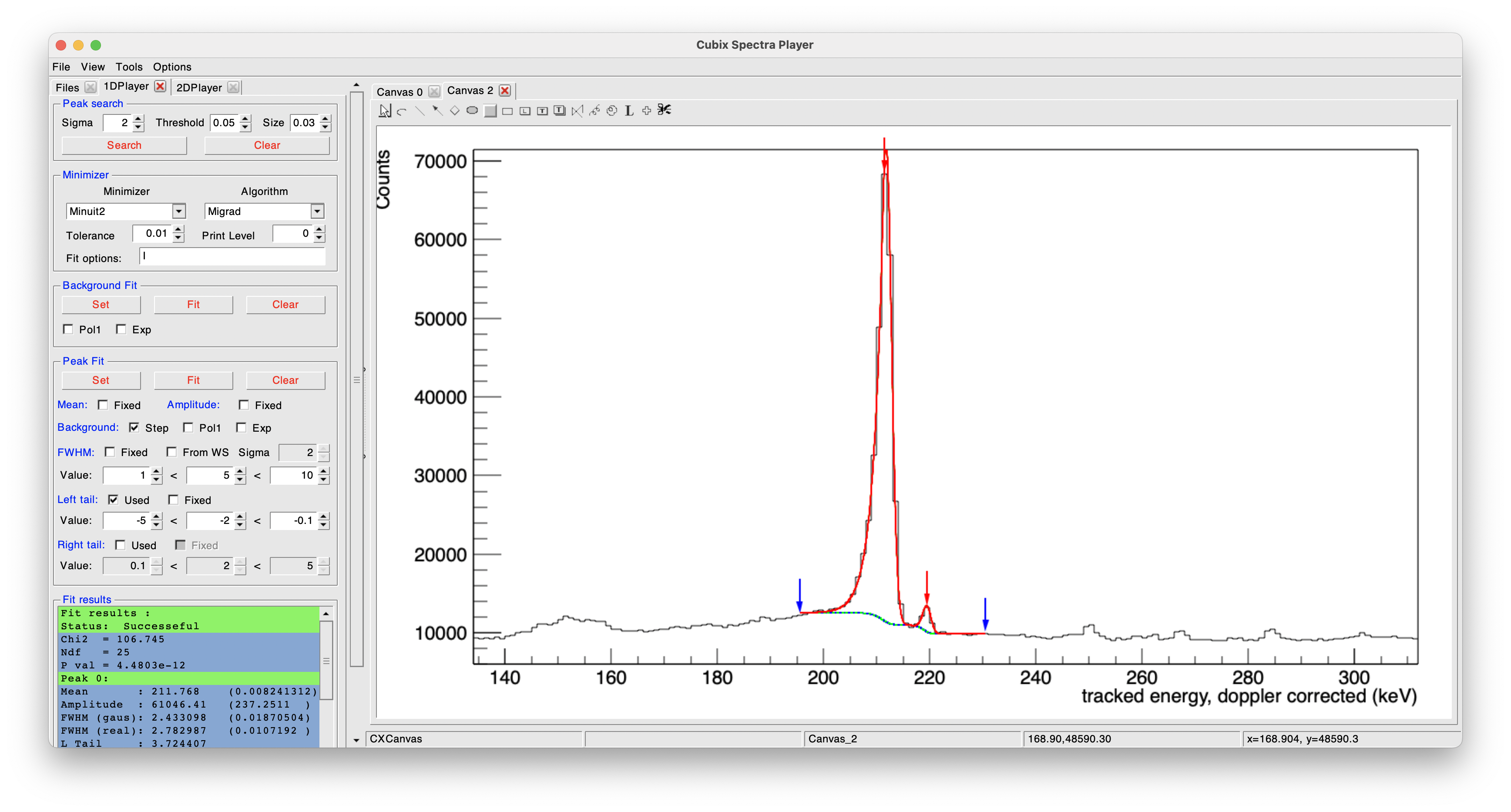
The following parameters can be defined:
- Mean: fix the peak centroid to the arrow value
- Amplitude: fix the maximal amplitude to one of the histogram at the arrow position
- Background: (multiple options possible)
- Step: stepped function bellow the peak (default)
- Pol1: polynomial function of order 1 (ax+b)
- Exp: exponential background
- FWHM:
- Fixed: Fix the FWHM at the defined value
- From WS: Use the FWHM function of the detector (if defined in the current Workspace)
- Sigma: If From workspace is activated, define the number of sigma to take as FWHM uncertainty
- Range: define the limits for the FWHM (if not using the workspace FWHM function)
- Left tail:
- Used: Fit with a left tail
- Fixed: Fix the left tail at the value defined bellow
- Range: define the limits for the left tail
- Right tail: (identical to left tail)
Note on peak fit results#
once a peak fit is performed, the peak(s) properties will be printed in the cubix pad Fit results and in the terminal. More details are printed in the terminal, such as this output:
****************************************
Minimizer is Minuit2 / Migrad
Chi2 = 59.0554
NDf = 60
Edm = 1.47489e-05
NCalls = 237
NumberOfPeaks = 1 (fixed)
BkgConst = 72.976 +/- 1.40616 (limited)
BkgSlope = 0 (fixed)
BkgExp = 0 (fixed)
Height_0 = 5793.94 +/- 48.2492 (limited)
Position_0 = 366.468 +/- 0.0129239 (limited)
FWHM_0 = 4.20073 +/- 0.0269407 (limited)
LeftTail_0 = -1.80514 +/- 0.0804794 (limited)
RightTail_0 = 5 (fixed)
AmplitudeStep_0 = 0.0122438 +/- 0.000589482 (limited)
Fit results :
Status: Successeful
Chi2 = 59.0554
Ndf = 60
P val = 0.510251
Peak 0:
Mean : 366.4684 (0.0129239 )
Amplitude : 5793.941 (48.24919 )
FWHM (gaus): 4.20073 (0.02694069)
FWHM (real): 4.200558 (0.02545712)
L Tail : 1.850239
R Tail : 1.822533
Area : 26110.08 (274.4399 )
E680 area : 14475.75 (167.3884 )
First, the minimizer used and the result of the minimization for the different parameters are printed, with the minimizer status, \(\chi^2\), and p value.
Then, more details information are listed on the peaks fitted. The area of the peak is derived from its analytical form. In the case of purely gaussian peak, the integral is defined by:
where N is the peak area and \(H\) is the amplitude of the peak. In the case of tailled gaussian, a specific calculation is done to include in the integral the contribution of the tails.
The uncertainty on the area is then derived from this equation, using the fit parameters errors from the minimization.
If the efficiency function is defined in the current workspace, the peak areas will be printed as real counts and corrected from efficiency in the terminal and in the cubix window.
Energy calibration#
The energy calibration utility is used to determine the energy calibration parameters of a \(\gamma\)-ray spectrum. This is done using the original RecalEnergy program of the AGATA collaboration developped by Dino Bazzacco. It can also be used to extract and fit the resolution function that can then be used in the detector's Workspace.
source definition#
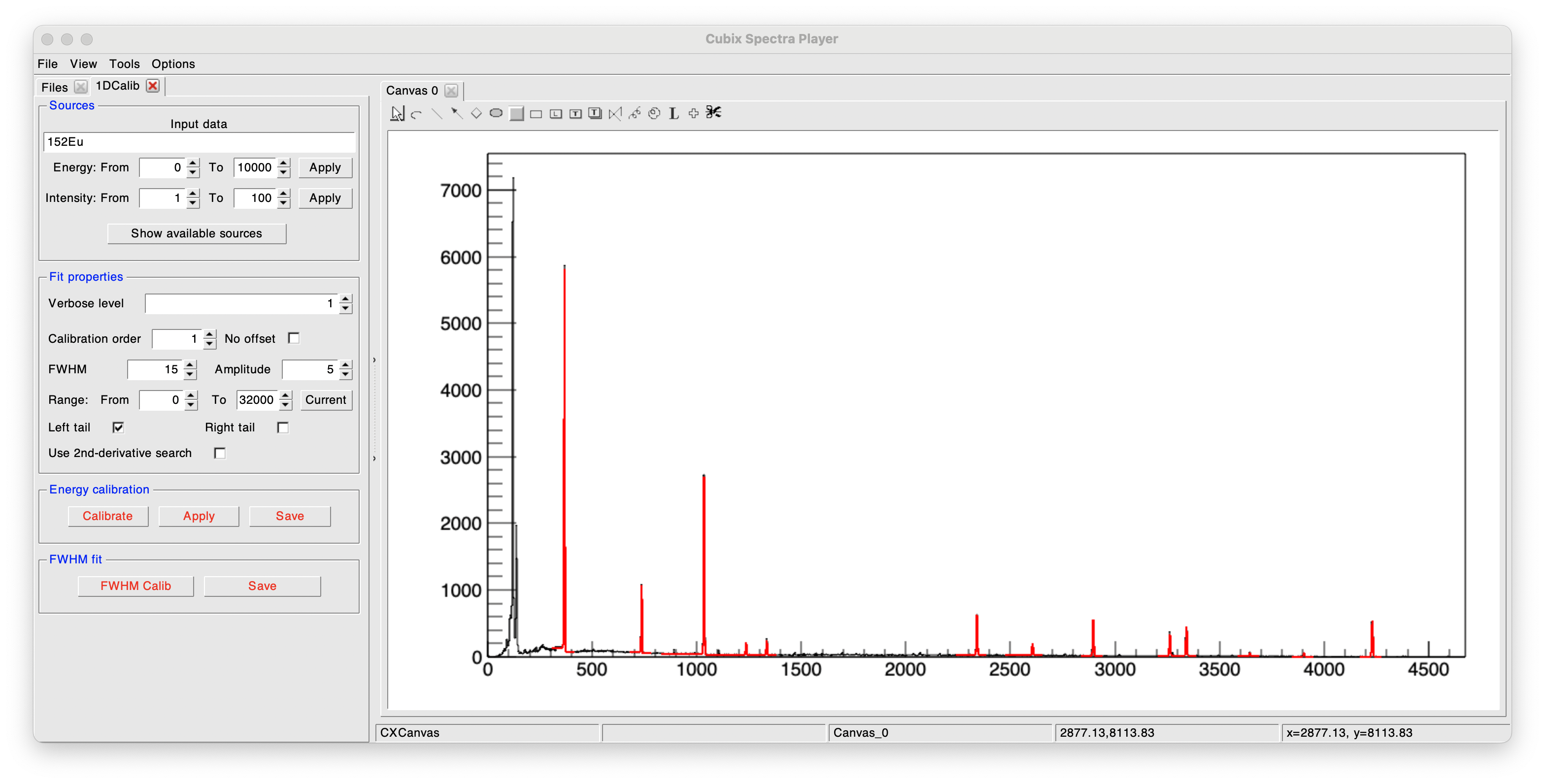
To show the availaible sources, click on Show available sources, this will print in the terminal such a message:
-- INFO : Sources availbale (including intensities):
133Ba 134Cs 152Eu 22Na 241Am 56Co 57Co 60Co 88Y
-- INFO : Calibration dataset availbale (only energies):
137Cs 208Pb 226Ra 28Al 40K
The sources that are including intensities can be used for efficiency fits (see Efficiency fits). For energy calibrations, all sources can be used.
The source files used are in $CUBIX_SYS/databases/Sources and can be adapted/modified/created. Here is an example of the 152Eu.sou source file:
#Generated from http://www.nndc.bnl.gov/nudat3/indx_dec.jsp with conditions:
#
#Nucleus = 152Eu
#T1/2 > 1y && < 1e10y
#DecayMode = Disabled
#Radiation Type = Gamma
#Radiation energy > 10keV && < 10000keV
#Radiation intensity > 0.1% && < 100%
#Ordering = Z, A, T1/2, E
#Output = Formated File
#Uncertainties = Standard style
#
Dec Mode Daughter Rad Ene. Unc Rad Int. Unc
EC 152SM 121.7817 3.0E-4 28.53 0.16
EC 152SM 244.6974 8.0E-4 7.55 0.04
EC 152SM 295.9387 0.0017 0.440 0.004
EC 152SM 329.41 0.05 0.1213 0.0024
B- 152GD 344.2785 0.0012 26.59 0.2
B- 152GD 367.7891 0.002 0.859 0.006
B- 152GD 411.1165 0.0012 2.237 0.013
EC 152SM 416.02 0.03 0.1088 0.0019
EC 152SM 443.9606 0.0016 2.827 0.014
EC 152SM 444.01 0.17 0.298 0.011
EC 152SM 488.6792 0.002 0.414 0.003
B- 152GD 503.467 0.009 0.1524 0.002
EC 152SM 563.986 0.005 0.494 0.005
EC 152SM 566.438 0.006 0.131 0.003
B- 152GD 586.2648 0.0026 0.455 0.004
EC 152SM 656.489 0.005 0.1441 0.0022
EC 152SM 674.64 0.14 0.169 0.003
B- 152GD 678.623 0.005 0.473 0.004
EC 152SM 688.670 0.005 0.856 0.006
EC 152SM 719.346 0.007 0.250 0.008
B- 152GD 764.88 0.04 0.189 0.004
B- 152GD 778.9045 0.0024 12.93 0.08
EC 152SM 810.451 0.005 0.317 0.003
EC 152SM 841.574 0.005 0.168 0.003
EC 152SM 867.380 0.003 4.23 0.03
EC 152SM 919.337 0.004 0.419 0.005
EC 152SM 926.31 0.05 0.272 0.003
EC 152SM 963.367 0.007 0.140 0.006
EC 152SM 964.057 0.005 14.51 0.07
EC 152SM 1005.27 0.05 0.659 0.011
EC 152SM 1085.837 0.01 10.11 0.05
B- 152GD 1089.737 0.005 1.734 0.011
B- 152GD 1109.18 0.05 0.189 0.006
EC 152SM 1112.076 0.003 13.67 0.08
EC 152SM 1212.948 0.011 1.415 0.008
EC 152SM 1249.94 0.05 0.187 0.003
EC 152SM 1292.78 0.05 0.101 0.003
B- 152GD 1299.142 0.008 1.633 0.011
EC 152SM 1408.013* 0.003 20.87 0.09
EC 152SM 1457.643 0.011 0.497 0.004
EC 152SM 1528.10 0.04 0.279 0.003
This ".sou" extension file is for sources with intensities (for efficiency fits, see Efficiency fits).
The ".cal" extensions are much more simpler, this is only a list of energies, as in the following example of \(^{28}\)Al source:
30.6382
104.62
212.017
271.175
314.733
831.45
846.764
983.02
1622.87
1778.969
1810.726
2282.773
2590.244
3033.89
3465.07
4133.408
4259.539
4733.847
6702.034
7213.034
7724.034
an energy can be commented using a "#". For printouts, a reference peak is used. By default this is the highest energy value. It can be changed adding a "*" after the energy of the desired \(\gamma\)-ray in the source file (see in the \(^{252}\)Eu exemple for 1408 keV transition).
Once one or more source has been defined in the Input Data text entry, it is possible to manually add energies by adding " -ener E" in the text entry.
It is also possible to remove entries by adding " -remove E". The energy needs to be given with a precision of 1 keV to be removed.
Finally, it is possible to manually define the reference peak by adding " -ref E" in the text entry, here also with a precision of 1 keV.
fit options#
Some fit properties can then be defined:
- Verbose: define the verbosity of the fit process:
- 0: only print the calibration parameters
- 1: print the fit options summary and the results on the reference peak
- 2: print the results on all the peaks that have been found
- 3: print also the residues of each peaks
- Calibration order: define the calibration polynomial order to be applied. Select "No offset" to remove the order 0 offset (a0)
- FWHM: width used for the peak search
- Amplitude: given in %, minimal amplitude of a peak to be taken into account
- Range: range to be used for the peak search (click on "Current" to apply the current range)
- Tails: apply or not left/right tails in the peak fit
- 2nd derrivative search: Can be used in case of complicated peak search
calibration#
Clicking on the "Calibrate" button will print the fit results of each peaks:
It will also open a new canvas showing on the top the calibration function and bellow the residual plot:
Finally, the output, as a function of the verbosity selected, will be printed in the terminal:
Clicking on the Apply button will apply the current calibration.
Clicking on the Save button will save the current calibration function in the desired Workspace.
Resolution fit#
It is also possible to fit the detector's resolution by clicking on the FWHM Calib buton:
Clicking on the Save button will save the current FWHM function in the desired Workspace.
Calibrate a list of detector#
Cubix allows to calibrate a list of detector (or channels) in one command. For this, it needs to take as input a two dimension histogram representing the energy in channel on the X axis as a function of the detector id on Y axis.
To use this tool, just plot the bidim in the cubix canvas, and open the Calibration tool:
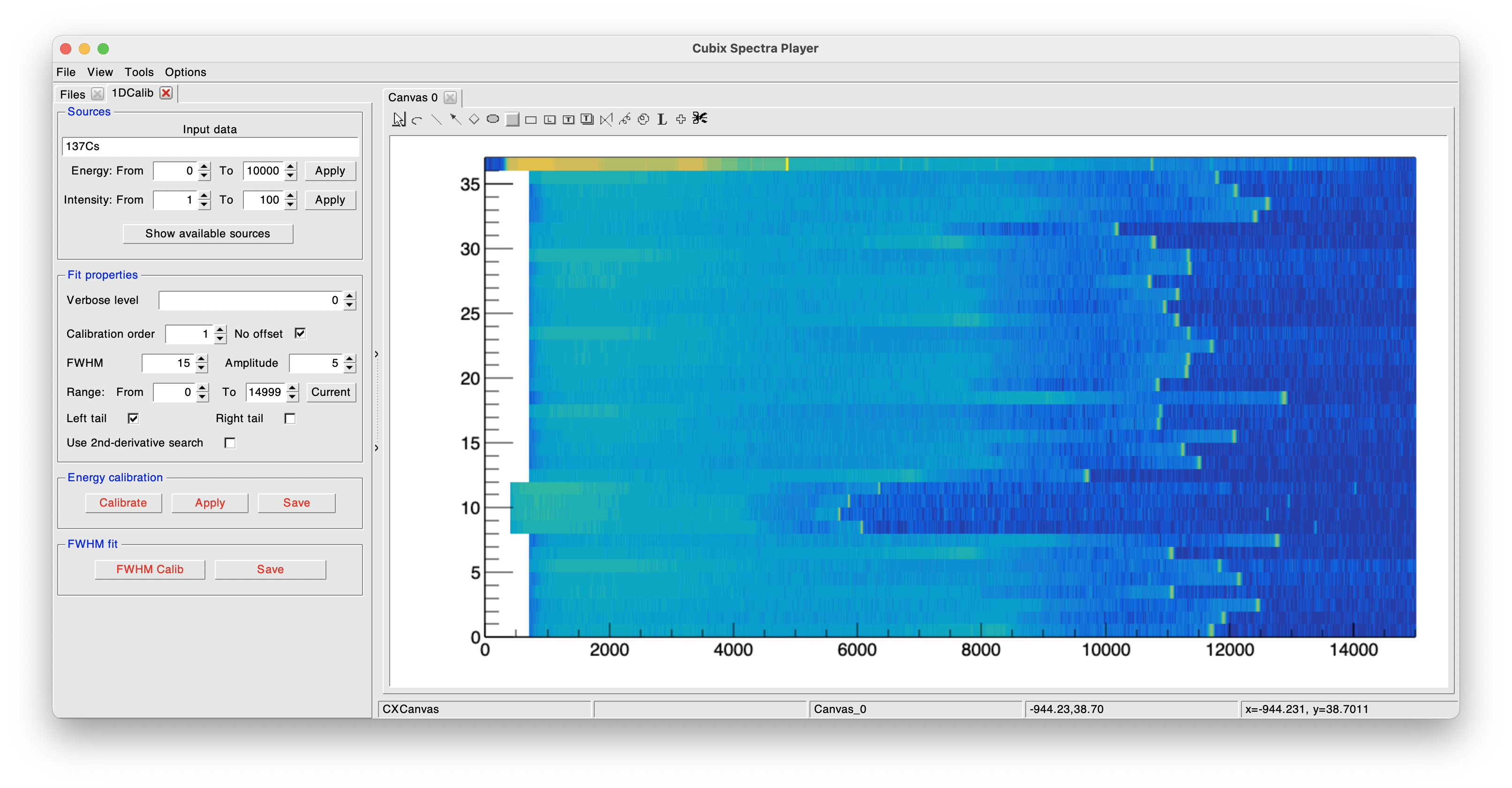
You can then define your peak search and press the calibrate button. This will plot the resulting FWHM for each id in a separate canvas:
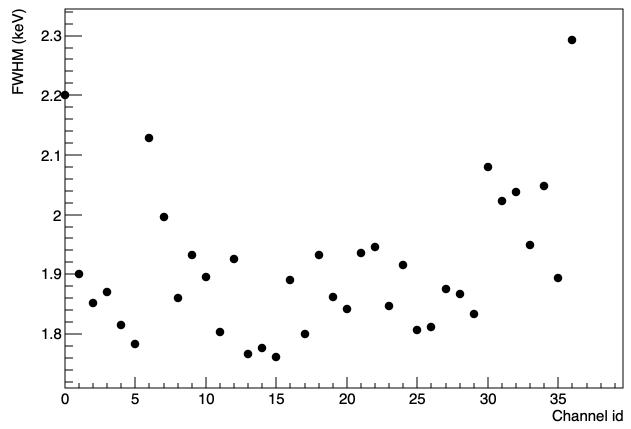
If you want to extract the calibration parameters, define the verbosity at 0. The result will be printed as follows in the terminal:
SegEvsIdM1_0: 0.000000e+00 5.649323e-02
SegEvsIdM1_1: 0.000000e+00 5.558890e-02
SegEvsIdM1_2: 0.000000e+00 5.312231e-02
SegEvsIdM1_3: 0.000000e+00 5.977824e-02
SegEvsIdM1_4: 0.000000e+00 5.446056e-02
SegEvsIdM1_5: 0.000000e+00 5.588739e-02
SegEvsIdM1_6: 0.000000e+00 5.982343e-02
SegEvsIdM1_7: 0.000000e+00 5.182992e-02
SegEvsIdM1_8: 0.000000e+00 1.090278e-01
SegEvsIdM1_9: 0.000000e+00 1.159412e-01
SegEvsIdM1_10: 0.000000e+00 1.128605e-01
SegEvsIdM1_11: 0.000000e+00 1.041865e-01
SegEvsIdM1_12: 0.000000e+00 6.817337e-02
SegEvsIdM1_13: 0.000000e+00 5.748102e-02
SegEvsIdM1_14: 0.000000e+00 5.883428e-02
SegEvsIdM1_15: 0.000000e+00 5.479455e-02
SegEvsIdM1_16: 0.000000e+00 6.094887e-02
SegEvsIdM1_17: 0.000000e+00 6.078302e-02
SegEvsIdM1_18: 0.000000e+00 5.136183e-02
SegEvsIdM1_19: 0.000000e+00 6.103431e-02
SegEvsIdM1_20: 0.000000e+00 5.851552e-02
SegEvsIdM1_21: 0.000000e+00 5.839151e-02
SegEvsIdM1_22: 0.000000e+00 5.650289e-02
SegEvsIdM1_23: 0.000000e+00 5.834277e-02
SegEvsIdM1_24: 0.000000e+00 5.931352e-02
SegEvsIdM1_25: 0.000000e+00 6.040048e-02
SegEvsIdM1_26: 0.000000e+00 5.929269e-02
SegEvsIdM1_27: 0.000000e+00 6.178512e-02
SegEvsIdM1_28: 0.000000e+00 5.828467e-02
SegEvsIdM1_29: 0.000000e+00 5.836988e-02
SegEvsIdM1_30: 0.000000e+00 6.137587e-02
SegEvsIdM1_31: 0.000000e+00 6.499680e-02
SegEvsIdM1_32: 0.000000e+00 5.330287e-02
SegEvsIdM1_33: 0.000000e+00 5.246363e-02
SegEvsIdM1_34: 0.000000e+00 5.469901e-02
SegEvsIdM1_35: 0.000000e+00 5.608943e-02
SegEvsIdM1_36: 0.000000e+00 1.359838e-01
(in the above example, the option "No offset is used, explaining all the 0 values in the second column.)
Efficiency fit#
The efficiency fit utility is used to determine the response function of the detector as a function of the energy. The function used is the one off the Radware program defined as:
where \(x = log(E_{\gamma} / 100)\) and \(y = log(E_{\gamma} / 1000)\), with \(E_{\gamma}\) in keV
The \(Scale\) is a global scaling of the full function. \(A+B*x+C*x^{2}\) represents the low energy part (from 0 to the maximum of the curve). \(D+E*y+F*y^{2}\) represents the high energy part, and \(G\) corresponds to the curvature at the linking part between low and high energy parts.
source definition#
The source definition is the same than in the Energy calibration utility, with the limitation of only using ".sou" source files.
building efficiency curve#
If we want to fit the efficiency from a \(\gamma-ray\) spectrum, one first need to fit the peaks to build the efficiency curve. If we already have the efficiency curve and only need to fit it with the theoretical function, move to the section next section.
The peak search engine used behind is the same than for the Energy calibration utility.
The first step from a gamma source spectrum is to build the efficiency curve.
This is done by clicking on Build eficiency curve.
This will fit all the peaks of the selected source(s), determining its integral, and applying the source intensity of each transition to build the efficiency curve as:
A second window will be opened containing the efficiency curve:
It has to be noted that this plot has been drawn with the option Normalize to ref enabled.
This means that the plot drawn is a relative efficiency plot, with a value set at 1 for the reference energy peak.
Fit efficiency curve#
Either the efficiency curve has been created as described above, either the curve has been already created outside cubix. In this latter case, one just need to open it with Cubix (TGraph format) and draw it in the current canvas.
To fit the efficiency curve, it is advised to use the Auto fit button that performs the minimisation in three steps:
It first fits the low energy part, then the high energy part, and finally the curve linking both.
If the automatic process does not work as wanted, there is still the possibility to constrain manually the parameters and click on Fit for doing a single minimisation.
Once the fit is performed, the theoretical function and its error band is ploted. The following examples are showing the fit results obtained with and \(^{152}\)Eu (FIPPS array), and from a Geant4 calculation simulating a peak each 100 keV (AGATA array):
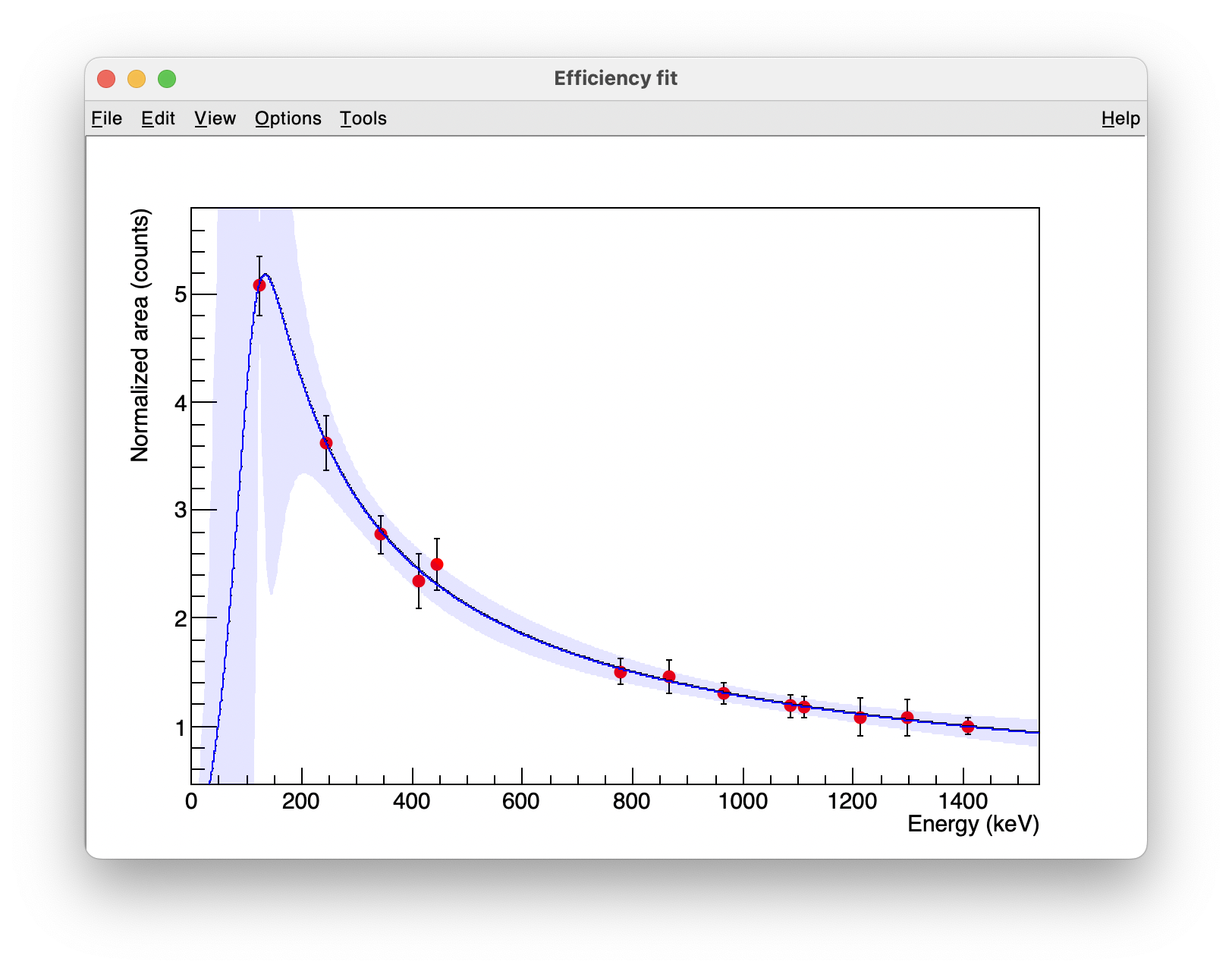
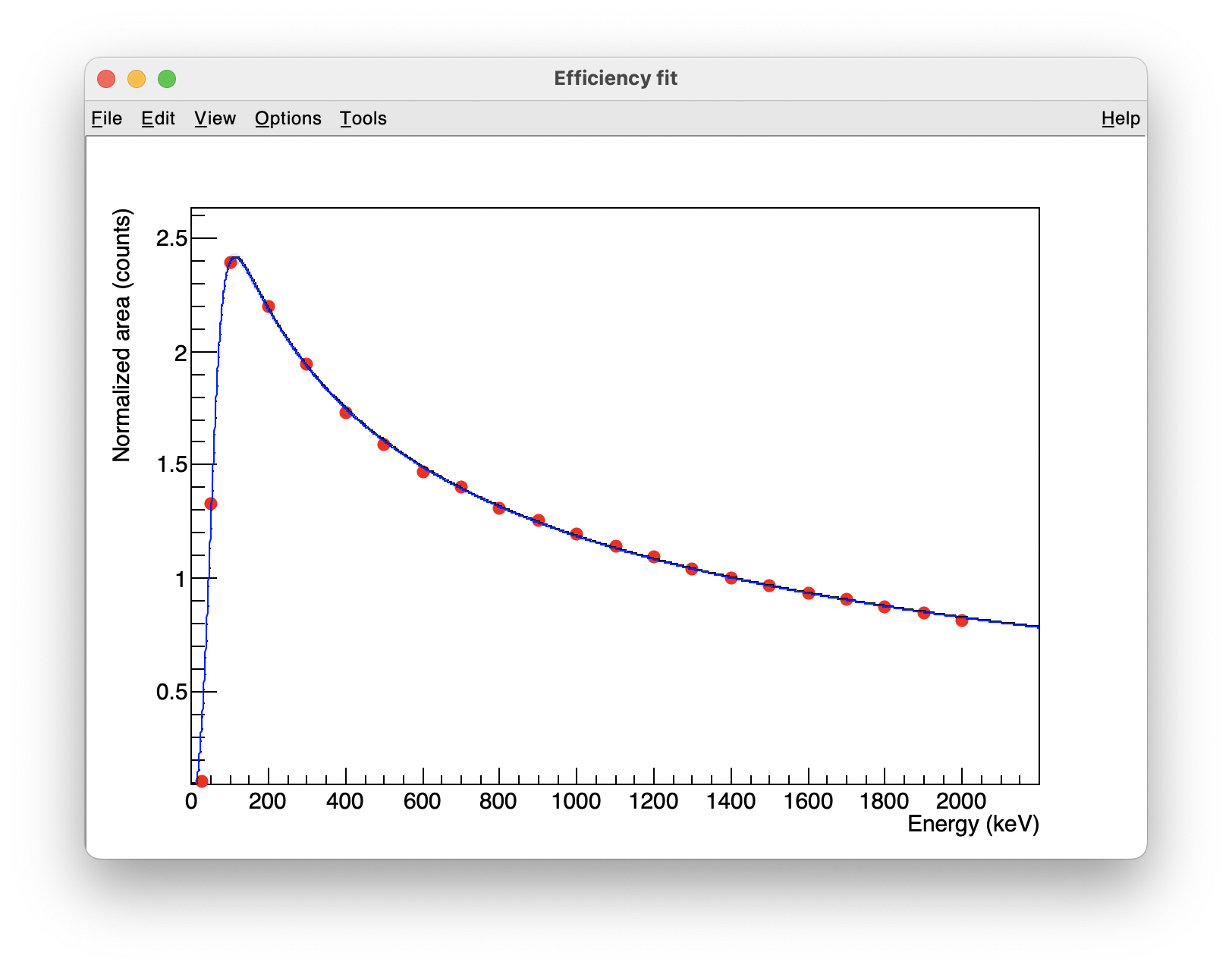
Once we are happy with the fit, it can be saved in a Workspace using the Save buton (see the workspace manager section for more details).
Background player#
The background spectra player allows for determining 1D and 2D backgrounds based on the ROOT TSpectrum classes.
- 1D background spectrum
When displaying a spectrum, click on "On" to show the standard background estimation. This can be adjusted by playing with the different parameters:
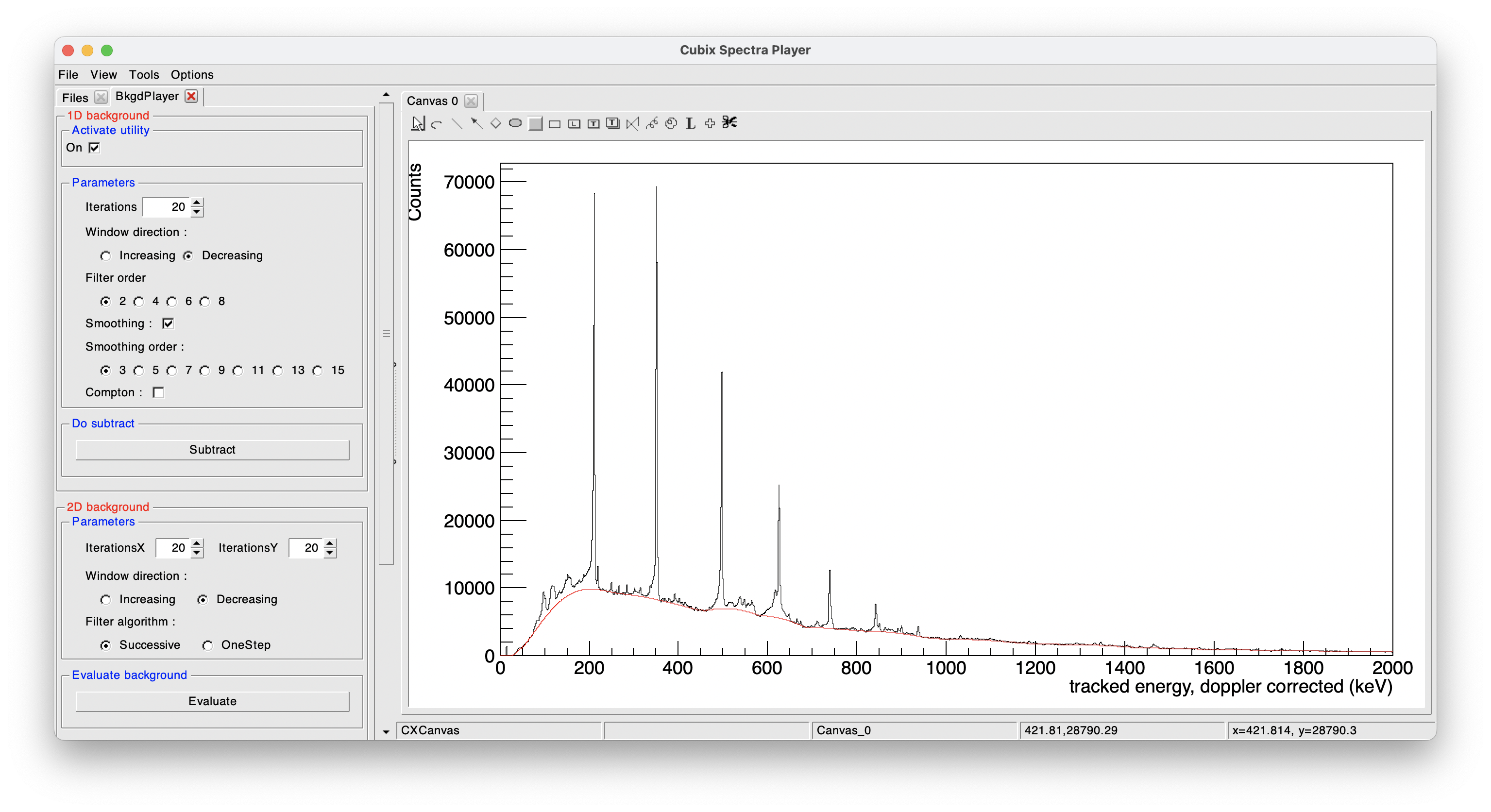
To subtract the background, click on "Subtract" and it will show the background subtracted spectrum:
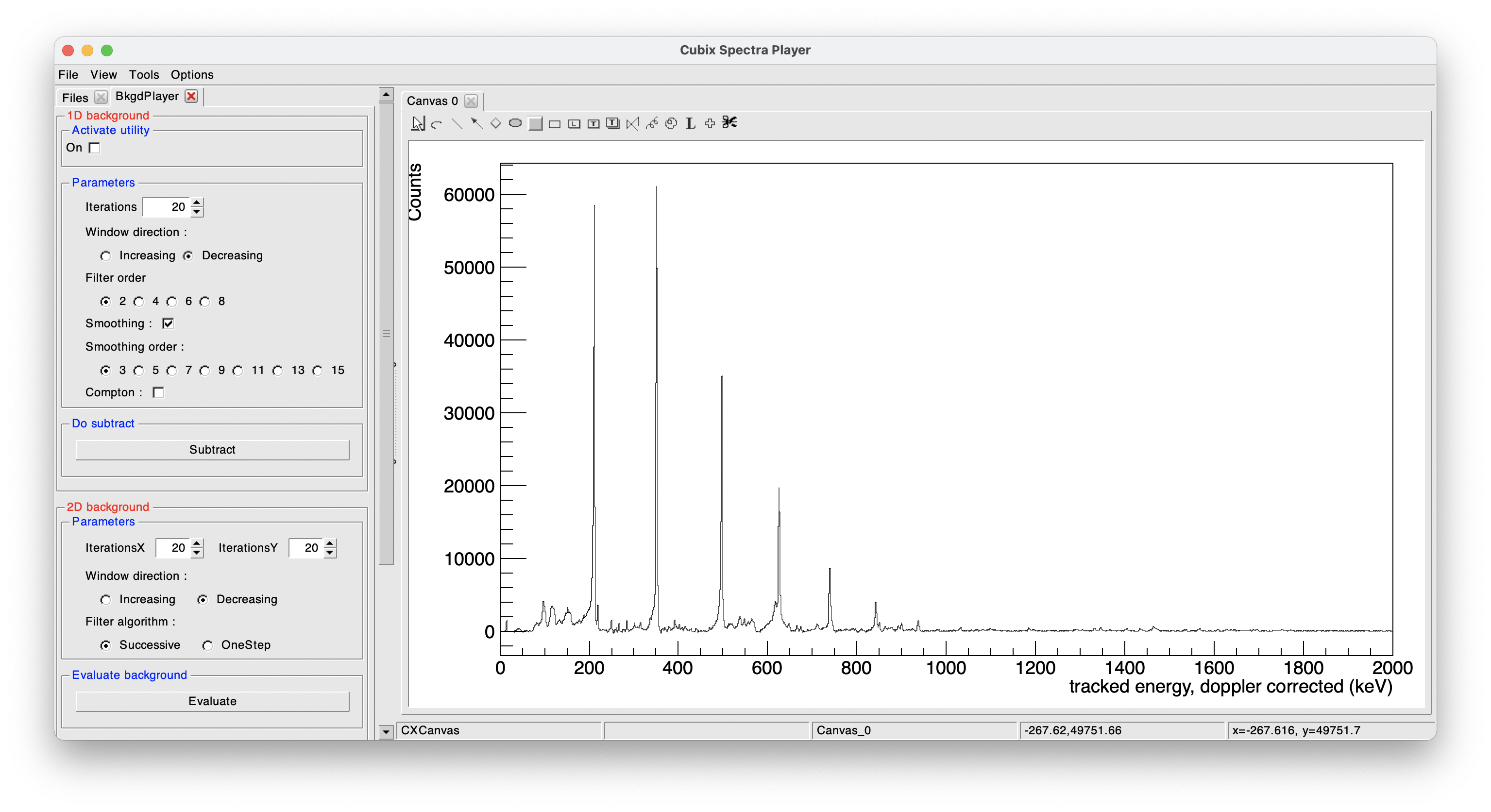
This tool need to be used carefully has this is a user-defined background. Peak area obtained on this kind of spectrum can differ to the one obtained on a fit performed on the original spectrum.
- 2D background spectrum
When displaying a 2D spectrum (namely a \(\gamma-\gamma\) matrix), click on "Evaluate" to start the 2D background evaluation. It will open a new canvas with on the top, the background subtracted 2D spectrum and bellow the remaining background:
The background subtracted 2D spectrum can then be used for a \(\gamma-\gamma\) analysis (see next section). Here again, be aware that the analysis quality can be affected by the way the background has been determined.
Angular correlation player#
The angular correlation player allows to plot the theoretical angular distribution between two correlated \(\gamma\)-rays, for given spins and mixing ratios.
It can also, for a given angular distribution that has been built from experimental data (in ROOT::TGraph format), fit the distribution to extract the experimental A2 and A4 parameters and perform the mixing analysis.
The player suppose a succession of two \(\gamma\)-rays, linking three levels of spins J1, J2 and J3 as in the following scheme:
The player looks like this:
The AngCorr tab is created after clicking on the New Instance button. It is composed of 4 sub canvases:
- top left: Theoretical distribution for the given spins and mixing value
- top right: 1D/2D mixing evaluation
- bottom left: display and fit of the experimental distribution
- bottom right: Chi2 minimisation of mixing values
When the AngCorr is open, double-clicking on a angular distribution in the TGraph format from the browser will directly plot this graph in the suited pad (botton left).
By default, we are assuming plots with an x axis in degrees.
If the experimental plot is in radians (range -1 ; 1 ), select the rad button before any fit of the distribution.
Correction factors setting/fitting#
Due to the finite size of the detectors, geometrical correction factors needs to be determine to be able to fit angular correlations with correct A2 and A4 values.
If known, the correction factors can be defined in the left pannel. As these parameters are experiment dependant, it can be saved with the Save Qi button in a workspace for not having to set the values for each cubix use.
If these parameters are not known, this tool allows to fit them on already well known transitions.
It is advised to find a physics case for which the A2 parameter is strong, and another one where the A4 is strong (if you don't have one with strong A2 and A4 parameters).
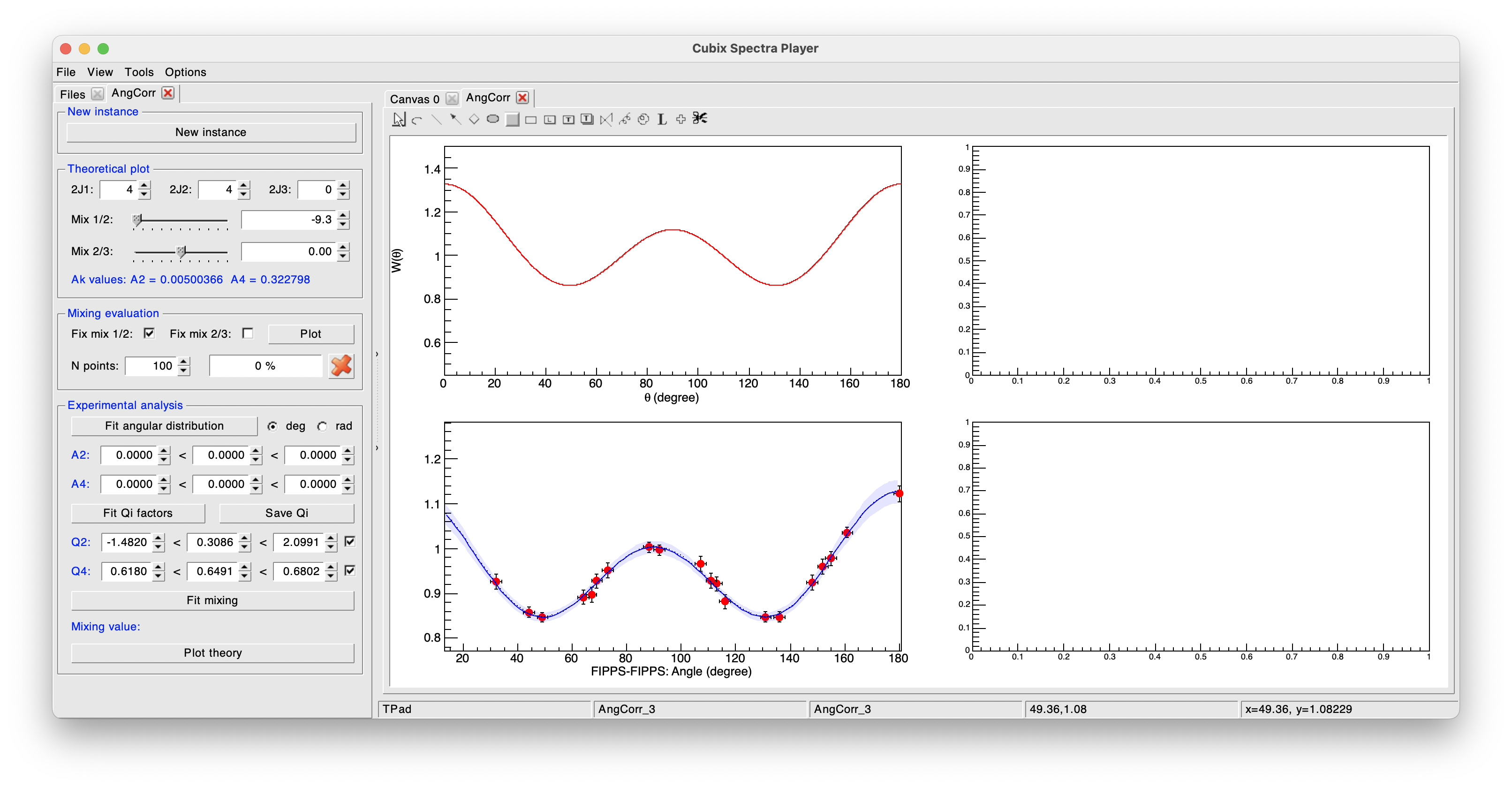
For example, here we will first fit the Q4 parameter on the transitions of 964 and 122 keV (\(2^{+}_{3} \rightarrow 2^{+}_{1} \rightarrow 0^{+}_{1}\)) of \(^{152}\)Sm measured from a \(^{152}\)Eu source.
The 964 keV transition has a known M1/E2 mixing of -9.3. We thus define in the player the spins and mixing value.
the spins needs to be defined as twice the spin (to have integer values for odd masses)
Once these values have been defined (see image bellow), the theoretical A2 and A4 values are shown in the left pannel.
We can indeed see that for this kind of transition, the A2 value is almost 0. The Q4 fit is then done by clicking on the Fit Qi factors button:
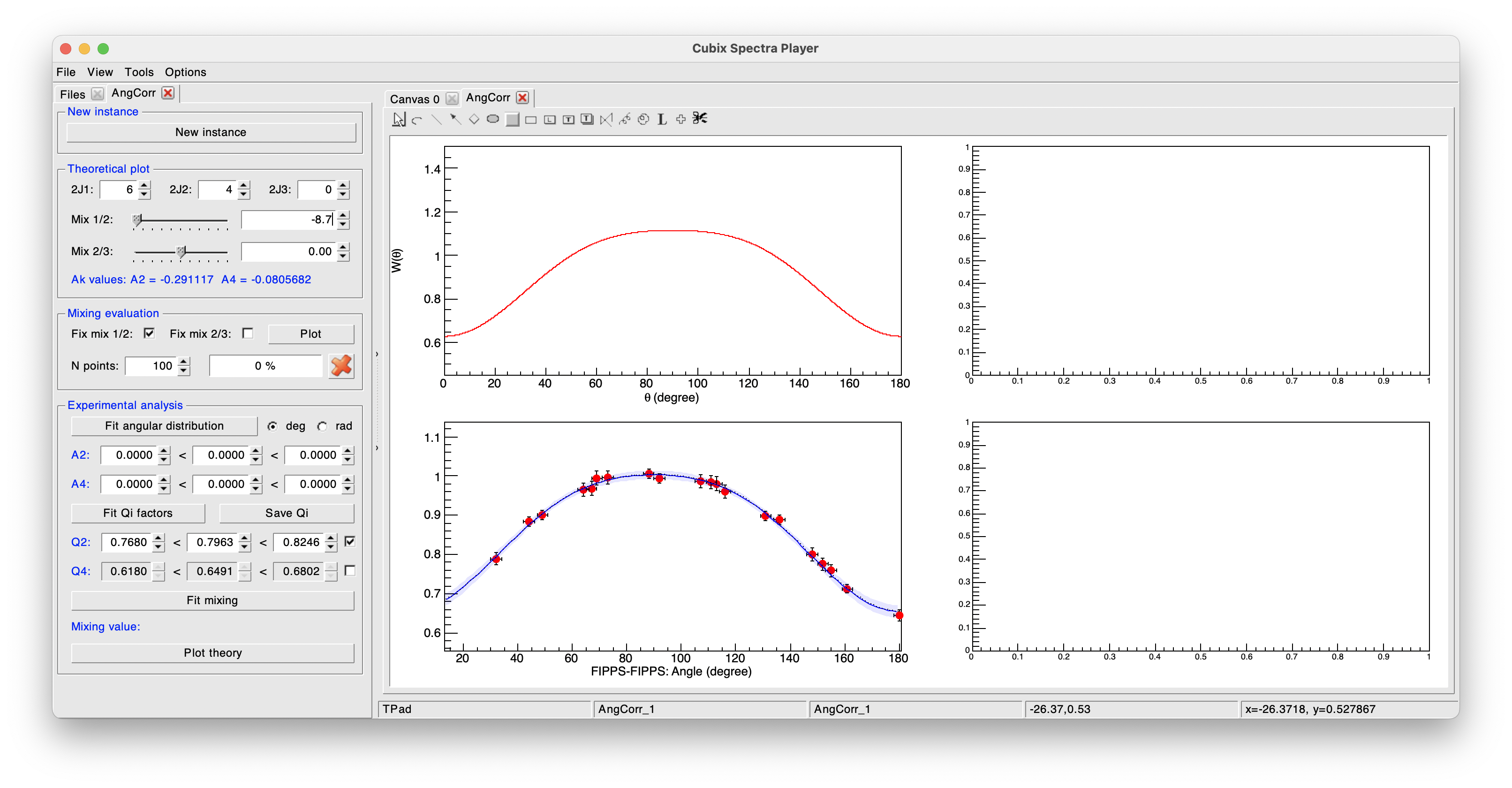
In a second step, we will fit the Q2 parameter on the transition of 1112 and 122 keV (\(3^{+}_{1} \rightarrow 2^{+}_{1} \rightarrow 0^{+}_{1}\)) of \(^{152}\)Sm measured from a \(^{152}\)Eu source. The 1112 keV transition has a known E2/M1 mixing of -8.7. We thus define in the player the spins and mixing value.
After setting these new values (see image bellow), we can see that here the theoretical A2 is much higher while A4 is almost 0.
To keep the Q4 value of the previous fit, we unselect the Q4 line to fix its value in the fit process (see image bellow).
The Q2 fit is then done by clicking on the Fit Qi factors button:
To check that the correction factors have been correctly defined, one can now fit the angular distribution by clicking on the Fit angular distribution button.
This will update the experimental A2 and A4 values in the left pannel.
Once the correction factrors have been defined, it can be stored in a Workspace to be saved on disk and automatically load with cubix for other angular correlation anaylsis of the same experiment.
This can be done using the Save Qi button.
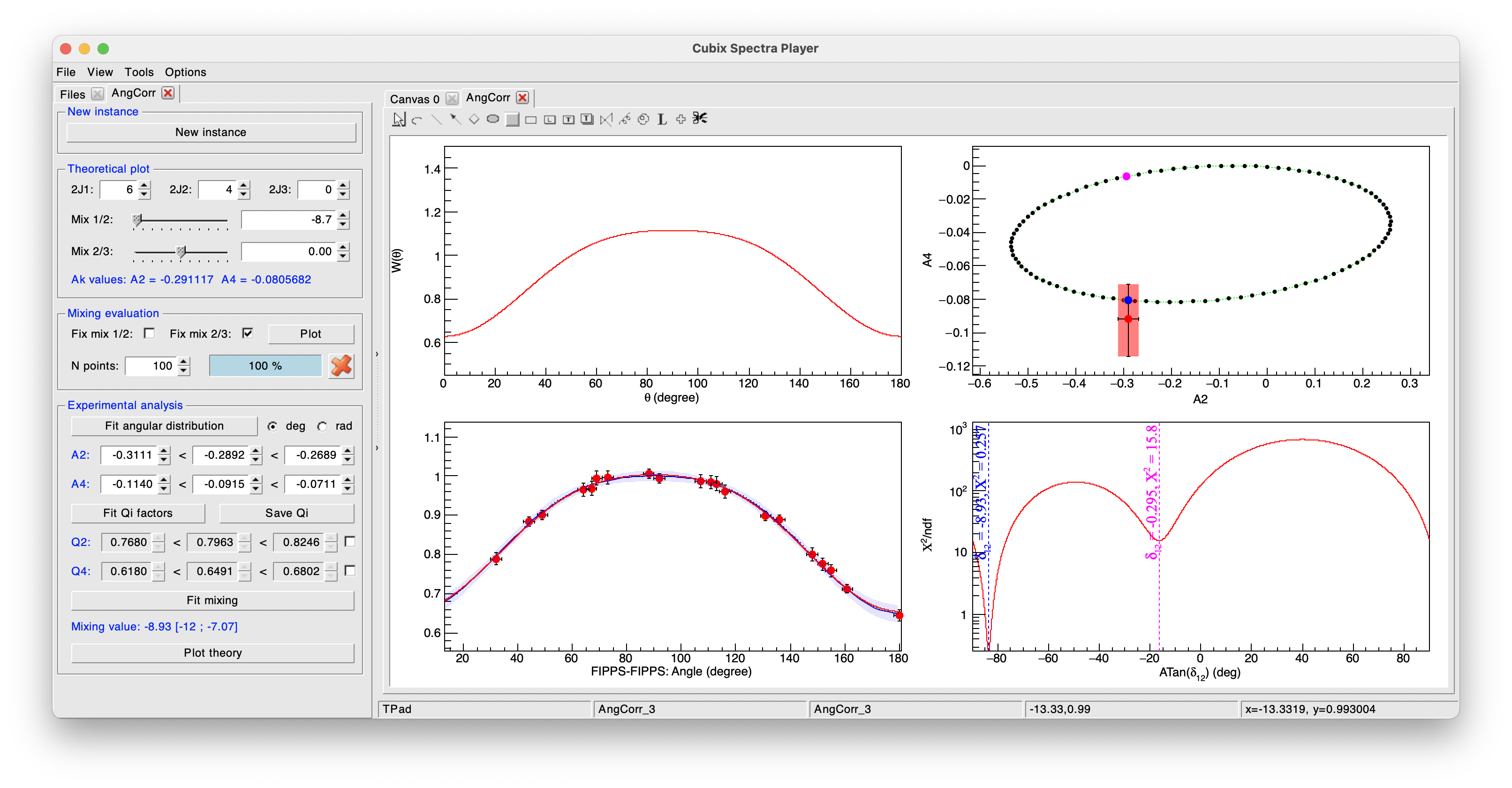
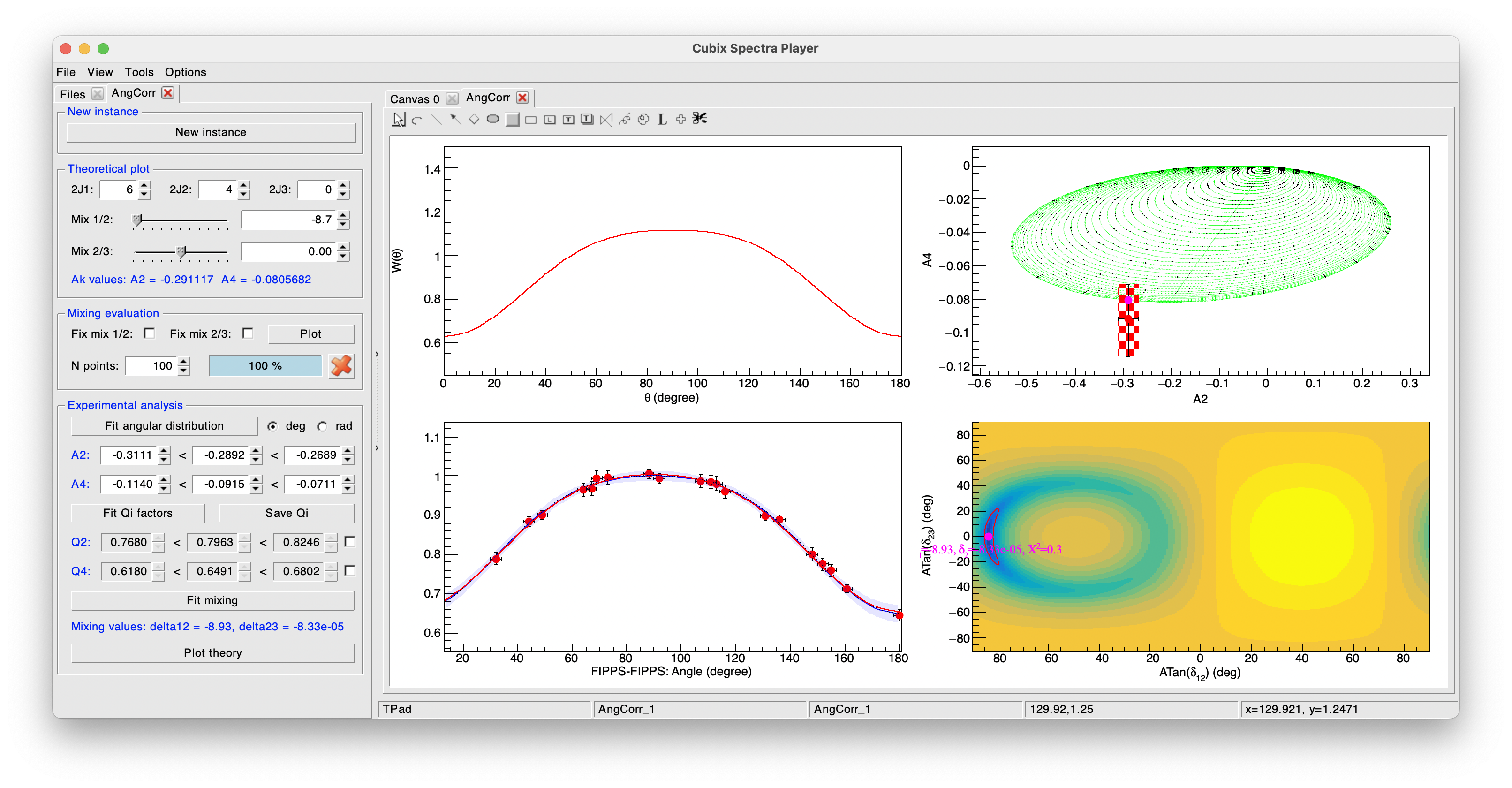
To check the consistency of our results, we can perform a mixing analysis:
1D mixing#
If we already know the mixing value of a transition, we can fix it in the Mixing evalation part of the left pannel.
Clicking on Plot will thus plot all the possible combinations of A2 and A4 for all the free mixing parameter in the top right pad.
The experimental point will be overimposed and a green point is also drawn corresponding to the mixing value of the theoretical plot (it can be changed in real time).
It is then possible to perform a \(\chi^{2}\) minimization to calculate the optimal mixing value by clicking on the Fit mixing button.
\(\chi^{2}\) plot will be drawn on the bottom right pad.
The possible minimas will be shown with the corresponding mixing and \(\chi^{2}\) values.
These minimas will also be reported on the top right pad to see what A2/A4 values it represents.
The mixing value corresponding to the first minimum will be printed in the terminal and in the left pannel bellow the Fit mixing button.
Its uncertainty can be calculated in two ways.
If the theoretical values of A2/A4 values for this mixing value are within the experimental error bars, the mixing uncertainties are the limits of mixing values that allow to stay within the error bars.
The other estimation is based on the \(\chi^{2}_{min}+1\) esimation.
The mixing values, around the minimum, corresponding to a \(\chi^{2}\) of \(\chi^{2}_{min}+1\) are used as mixing uncertainty.
These two uncertainties values are printed in the terminal.
Finally, it is possible to overlay on the experimental distribution the theoretical distribution corresponding to the current spins and mixing values by clicking on the Plot theory button.
This will over impose the theoretical plot, renormalized to the A0 parameter of the experimental distribution and using the defined correction factors.
All these elements can be seen on the following figure:
2D mixing#
If we don't know anything about the mixing value of both transitions, a 2D mixing can be done.
this kind of study will much likely give very large uncertainties because of the huge number of mixing combinations than can give the same A2/A4 values.
We need here to free both transition mixing in the Mixing evaluation part. Clicking on Plot will now represent a much more complicated graph of A2 and A4 combinations (see bellow).
Here again, we can then process the \(\chi^{2}\) 2D minimization to calculate the optimal mixing values by clicking on the Fit mixing button.
The result will be a two dimensional function (one axis per transition mixing).
The point corresponding to the lowest \(\chi^{2}\) is drawn with its corresponding mixing values.
Here also, a \(\chi^{2}_{min}+1\) esimation is done. The contour corresponding to all values with a \(\chi^{2}\) of \(\chi^{2}_{min}+1\) is drawn in red.
The mixing values corresponding to the lowest \(\chi^{2}\) are printed in the terminal and in the left pannel. No uncertainty is calculated at this level due to the complexity of its representation.
All these elements can be seen on the following figure:
examples#
Once the correction factors have been correctly defined, one can make the angular correlation study of other transitions.
The following example is still from an \(^{152}Eu\) source: the transitions of 689 and 122 keV (\(2^{+}_{2} \rightarrow 2^{+}_{1} \rightarrow 0^{+}_{1}\)). The mixing of the 689 keV is known to be \(\delta(E2/M1) = +19 \pm 5\).
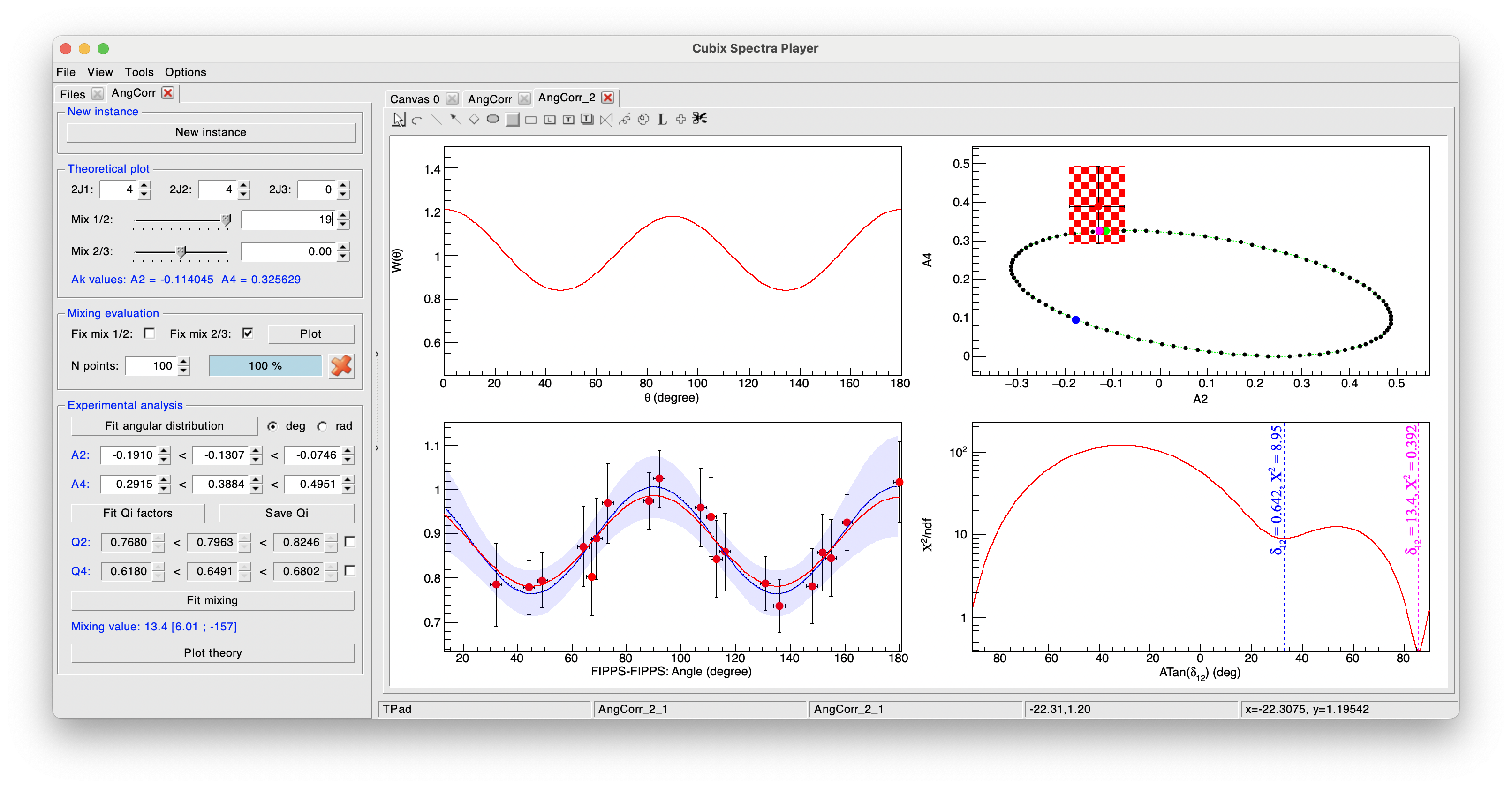
The results obtained is in good agreement with the literature with a mixing value determined as \(\delta(E2/M1) = +13.4 \pm 7.4\).